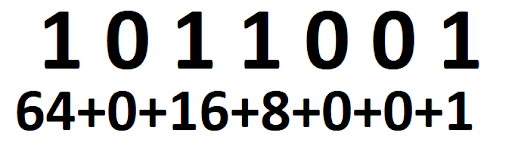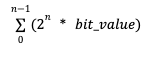Introduction to Binary Numbers
We’ve all seen it before. You put in that new fast 1 TB SSD only to find it has 931GB of space. What happened to that other 69 GB of storage? That is another 20,000+ songs from your itunes library you won’t be able to fit. This has to do with how computers calculate capacity vs how we as humans market products. This is where the binary system vs decimal system comes into play.
Binary
If you ever heard the phrase, “computers work in 1’s and 0’s” that is because they do. Each number or letter is some series of 1’s and 0’s. 0 is 0, 1 is 1, but after that it gets complicated. But then 2 is (10), 3 is (11) and 4 is (100). This system is referred to as base 2, so the calculations will primarily be built on that. Everything is multiplied by 2. So remember this: 1, 2, 4, 8, 16, 32, 64. So how this works is, let’s take the binary number of 1011001 and figure out what it equals. If there is a 1 there, you add the base 2 number, if there is a zero then it is excluded.
There is a lot to unpack here …
How to convert binary numbers to decimal
A bit is a binary digit that can either have a value of 0 or 1. To convert a binary number to a decimal you can either start from the top left or the top right bit and, for each bit, apply the following formula:
2ˆn * bit_value
(two raised at the position of the bit, multiplied by the bit value)
Where:
- n is the position of the bit, where n starts from 0 in the top right position
- and bit_value is either 0 or 1
The resulting decimal value will be the sum all the decimal numbers at each position:
If you want to simplify this equation there are 2 things to understand. What the 0’s and 1’s mean and how the second row of numbers come to be. The 0’s and 1’s simply mean either there is a digit for calculation or not. If there is a 0 then there is nothing to add. If there is a 1 there, there is a digital to add to find what the binary number equals. The second part is, starting from right and going left, each digit increases by a multiple of 2, starting with 1. So if this was 1111111 it would have been 64+32+16+8+4+2+1 (127), if it was 1000000 it would have been 64+0+0+0+0+0+0 (64). And if it was 1000001 then it would be 64+0+0+0+0+1 (65).
Weirdly enough, we calculate memory in multiples of 2s but more on that later.
Decimal
So decimal is based on 10 which is more or less how we do our mathematics for most of humanity. These values go from 0-9 and it is how we as humans essentially have done math for a very long time. This is also the format where we calculate even the most complex equations by hand.
So why is your 1 TB SSD only 931GB?
That actually is not as confusing as you may think. Remember the base 2 system we discussed before? This is where base 2 and base 10 start to have some separation. We’ve all heard of Megabytes, Gigabyte and Terabytes, they are designed in base 10. 1000MB=1GB and 1000GB=1TB. However that is for reporting purposes (marketing if you will), not how storage is calculated.
A Byte is the smallest measurement we typically deal with. Although there are bits, that will muddy the waters right now. 1,024 bytes = 1 Kilobyte (KB). Then 1024 KB = 1 Megabyte (MB), etc. So to figure this out, if 1TB is 10^12 Bytes or 1 Trillion Bytes, we have to convert that to GB. So you take 1,000,000,000 / 1,024^3), the 3 comes from how many times you have to divide 1024 to get from Bytes to Gigabytes. B>KB, KB>MB, MB>GB. So that number becomes 931GB.
Drawn out it looks like this (rounded decimals):
1,000,000,000,000 Bytes / 1024 = 976,562,500 KB
976,562,500KB KB / 1024 = 953,674 MB
953,674 MB / 1024 = 931 GB
What about Memory (RAM)
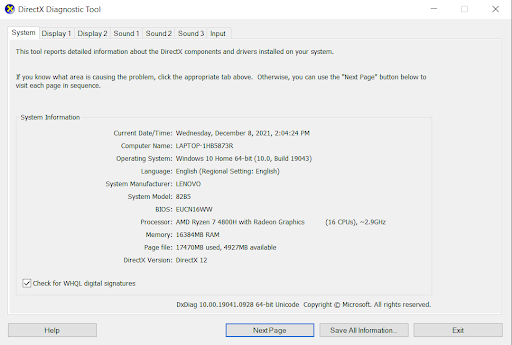
Funny enough, ram is the complete opposite. 2GB of ram is 2,048MB. Marketing does the opposite with memory where we take the actual amount and round down. So while most systems list 8 GB or 16 GB of memory, it is really 8,192 MB or 16,384 MB. To avoid confusion, Windows usually hides this from the users, but either in the BIOS screen or if you run DX Diagnostic tool, you can see the full amount.
What about Letters?
Well this one is tricky because the binary system has some overlap. For example, a capital “A” is in 8-bit encoding equal 01000001 which also happens to be equal to 65 in decimal. Different software and operating systems more or less have a binary subset table to differentiate how these are handled to make sure it calculates everything properly. And this is done over a billion times per second without error so do not be worried about this.
Hexadecimals?
So now we get to how this is applied a bit more in networking. If you recall in a previous blog where we talked about MAC Addresses, we use hexadecimals in those strings. Oftentimes you’ll see a “0x” in front of a series of digits, numbers or a combination of both. This signifies this is a hex or hexadecimal. In the case of MAC Addresses, it is usually 2 characters. DO NOTE, this table is vastly different than the binary table as anything past 9 is different, below is how to translate hex vs decimal vs binary:
| Hexadecimal | Binary | Decimal |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| A | 1010 | 10 |
| B | 1011 | 11 |
| C | 1100 | 12 |
| D | 1101 | 13 |
| E | 1110 | 14 |
| F | 1111 | 15 |
So you’ll notice to encode one hex you need 4-bit words or 2-digit words and like MAC Addresses, we will convert 8 characters down to 2. So if we take 10011110 and convert it, it will be 9 (1001) and E (1110) or 9E, but often written as 0x9E to distinguish that this is a hexadecimal. This is how your computer translates things like MAC Addresses into its core language.
Conclusion
Binary, decimal and even hexadecimal are very important concepts to understand. In practice, most of it is used by computers, communication systems, and some software languages (e.g. assembly). So it is good to understand the basics. But in reality, most people even in the tech space don’t actively use it on a daily basis. But at the very least, you know where that missing 69 GB of data went to!